Fraud-proof system
It is important to understand Optimistic rollups before diving into Fraud-proofs. We recommend reading this page on rollups.
Fraud-proofs are critical components in optimistic rollups. They allow anyone to challenge incorrect computations submitted off-chain and help ensure that only valid results are accepted on-chain, maintaining the integrity of the system without requiring every computation to be verified on-chain.
For instance, imagine a chess game engine hosted and running inside an off-chain execution environment on multiple nodes. It becomes critical for these off-chain nodes to prove the honesty of the result they submit to the underlying blockchain. In this context, a chess rollup would require a fraud-proof mechanism plugged with its game logic to achieve fairness and auditability.
Design Considerations
Designing a robust fraud-proof system involves balancing performance, decentralization, and security. Here are some core principles:
- Scales with number of participants: Supports any number of nodes without bottlenecks.
- Low cost to participate: Affordable for individuals to run a validator node.
- Permissionless access: Anyone can submit claims or challenges.
- Sybil resistance: Must be secure against attackers using fake identities.
- Fast dispute resolution: Minimal settlement delay is essential for usability.
Cartesi researchers have published two research papers on the fraud-proof mechanisms employed in the Cartesi stack namely Permissioned Refereed Tournament(PRT) and Dave. Let’s get a brief overview of the research and understand how these algorithms work.
The Core Idea
The key algorithm is as follows. Referee(the blockchain) and players(the node operators) must agree on a deterministic state transition function and on an initial state. The initial state of the machine contains all the information necessary to perform the desired computation and it can be summarized by the root hash of the Merkle tree. The players first compute the final state by successively applying the state transition function over the initial state. They then make a claim by submitting their results to the referee. If all players agree, the referee accepts the result as correct. Otherwise, the referee guides the players into a binary search that progressively bisects the computation to identify the earliest disputed state transition. Finally, by verifying this single state transition, the referee can identify and eliminate a dishonest player.
This core idea gets complex when the number of players increases, and the following algorithms try to address these issues.
Permissioned Refereed Tournament(PRT) Algorithm
PRT aims to tackle the sybil attack situation in a permissionless environment. A popular technique of proving the correctness of an execution is refereed games, which has been adopted by several layer-2 projects. This technique gives the base-layer the ability to efficiently referee a dispute between two layer-2 players that disagree on the result of a computation over layer-2 state.
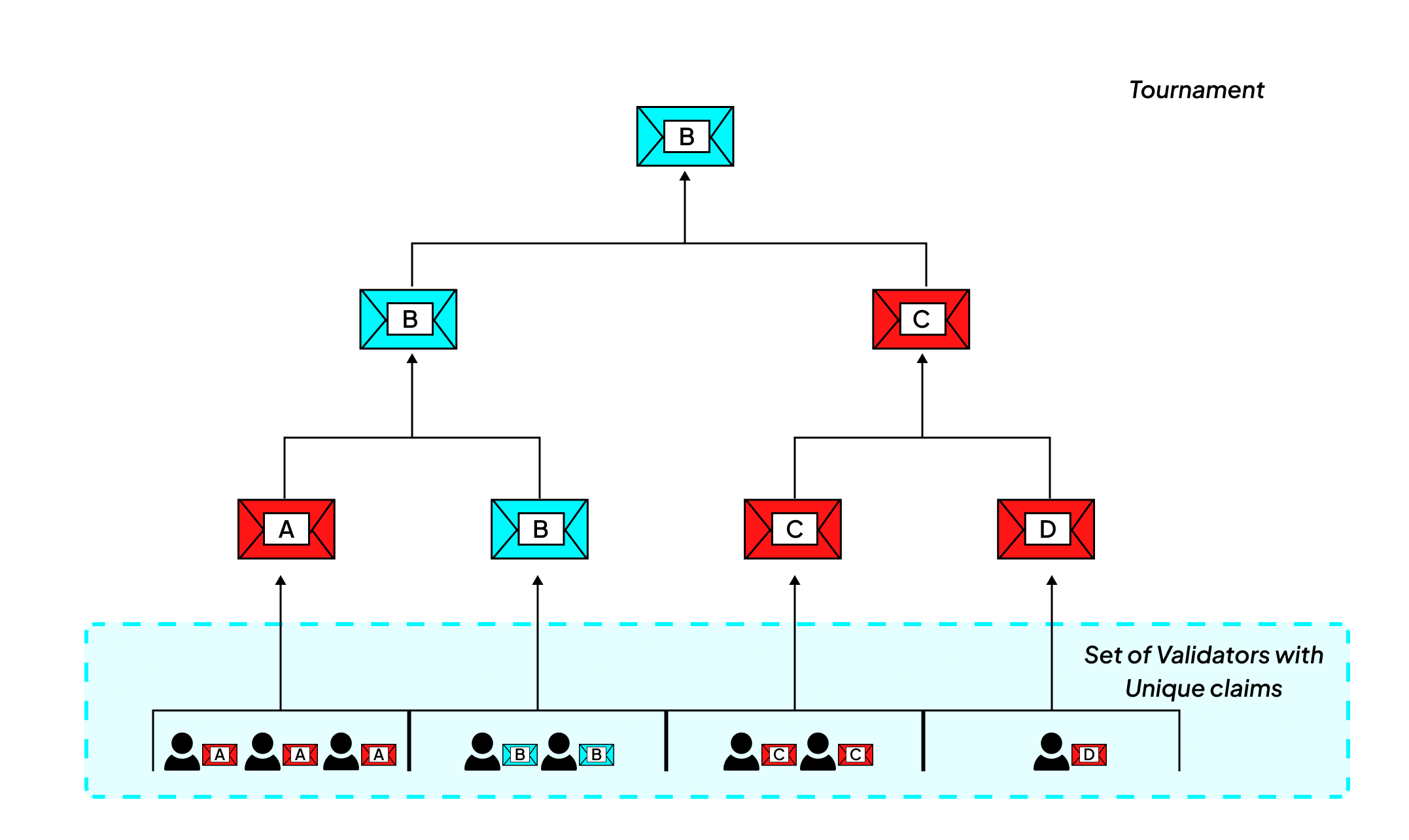
How it works:
- Claims are made using sparse computation hashes (snapshots of parts of a computation).
- Claims enter a tournament bracket where they’re progressively compared and eliminated.
- Disputes proceed in multi-stage rounds, and at each level the honest party only fights one match.
- Bonds are used to discourage dishonest claims, but they're kept affordable to preserve decentralization.
Refer Paper: https://arxiv.org/pdf/2212.12439
Dave Algorithm
Dave builds directly on the foundation laid by the PRT protocol, preserving its key strengths while significantly improving liveness and reducing settlement delays.
Improvements over PRT
One major innovation in DAVE is the use of dense computation hashes combined with validity proofs. This allows it to maintain strong guarantees against dishonest behaviour without the high overhead typically associated with dense proofs. Unlike PRT, which relied on a fixed tournament bracket and suffered from delays that scaled with the adversary’s ability to censor, DAVE introduces a dynamic dispute resolution mechanism that amortizes the adversary’s censorship budget across the entire dispute process. This results in a much smaller delay, with total settlement time growing logarithmically with the number of attackers, and with a smaller constant multiplier than PRT.
Additionally, DAVE employs a more sophisticated matchmaking strategy and introduces grace periods and demotion counts to prevent dishonest actors from stalling or manipulating the dispute process. These improvements make DAVE a more scalable, resilient, and responsive fraud-proof system for the next generation of rollups.
Refer Paper: https://arxiv.org/pdf/2411.05463
Industry-wide comparison
Research on Dave has quickly become one of the leading fraud proof systems in the optimistic rollups space. Below is a tabular summary of how it stands against other notable projects.
Credits: Fraud Proof Wars by L2Beat
| Project | Concurrency | Enforces Correct Bisections | Happy Case Bonds | Settlement Delay | Delay Attack | Resource Exhaustion Attack |
|---|---|---|---|---|---|---|
| Arbitrum Classic | Partial | No | 1 ETH | ~7d | Possible for indefinite time, requires little funds. May need one-off ordering control. | Not possible |
| Arbitrum BoLD | Full. Graph is shared between challenges | Yes | 3600 ETH | 7d | Up to 14d | Possible, requires ~7× defender’s funds (can increase to 10× or more) |
| Cartesi protocol (2 levels) | Partial (tournament) | Yes | 1 ETH | 7d | Possible for a limited time (few months) | In practice not possible (very costly) |
| Cartesi + ZK single step | Partial (tournament) | Yes | 1 ETH | 7d | Possible for a limited time (few months) | Not possible |
| OPFP | Full. Graph is shared between challenges | No | 0.08 ETH → increases up to ~700 ETH | 3.5d | Might be too short to coordinate defense under strong censorship attack | Possible, requires same or slightly fewer funds than defender |